
Keywords: I.3.3 image generation (rendering), I.3.7 ray tracing,
with applications in H.5.2 user interfaces, I.7.2 desktop publishing,
J.5 fine arts
Look alike images can be made by image processing techniques out of the pixel values of a two dimensional raster image. But to imitate copper plates a three dimensional scene description has to be used. In the last few years image generation techniques have been studied, especially how to generate photo realistic images from three dimensional scene descriptions. One of these techniques is the well known ray tracing algorithm[1,2,3] that generates photo realistic images with shadows, mirror and glass effects.
The following considerations have their target in generating images that resemble copper plates. In Section 2 the term copper plate is defined. Section 3 illuminates suitable image generation techniques, while in Section 4 the integration of these techniques in a ray tracer is presented. Section 5 deals with implementation details and presents some results. Before some conclusions are given, Section 6 shows how to use copper plates for generating icons for user interfaces.
Conventional copper plates are made by cutting lines into a metal sheet with the help of a graving tool. In the printing process these engraved lines are filled with paint, leaving the other parts clean. The colour is transfered to a sheet of paper when pressing the plate onto it. Three dimensional effects on the resulting figures are produced by the artist who draws the lines in a special manner and by hatchings. Besides the copper plates there are other, comparable techniques as etchings or woodcuts. More details on this subject are presented elsewhere[4].
In the following considerations the term copper plate refers to the result of the printing process, not to producing the printing sheet. A typical copper plate is therefore a drawing that consists of lines of varying thickness and of single points. It does not contain gray values. The objects represented are bordered by lines. The edges are partially more emphasized than the bare (realistic) presentation would afford. Shading is done by regular hatchings in several thicknesses and distances. Dashed lines and interspersed dots enlarge the spectrum of possibilities.
Often letters, sometimes longer explanations are included in the image. Sometimes invisible objects that are occluded by others are drawn with dashed lines. The copper plate technique is also used to produce printable black and white clichées from gray scale images, in modulating the thickness of the lines in hatchings with the pixel values. The following discussion will face on the subject of imitating three dimensional copper plates algorithmically.
At first we should discuss how to represent copper plates. From an artists view a 2D object description would be convenient, e.g. using a spline description of the lines with some drawing attributes. Scan conversion has then to be done later. The advantage would be a resolution and device independent representation. But as it could be complex to determine the projection of general lines on surfaces we chose a raster representation, and make use of standard rendering algorithms.
With image processing techniques all raster images can be handled, also such originated from a scanner, but the three dimensional scene information is not available when producing the hatchings. The two dimensional patterns can either be straight lines or follow border lines of the segmentation area, what is not satisfactory. As hatchings should express three dimensionality, a three dimensional model and a rendering algorithm should be used.
For imitating copper plates with computer algorithms, the geometry and colour part of a rendering algorithm has to deliver suitable information. Generally, there are two different kinds of image rendering algorithms, that generate images from three dimensional scenes: the image-centered and the scene-centered algorithms[1,6]. Scene centered algorithms project unoccluded objects onto the image plane and apply colours on these areas. For single objects the borders can be found easily. Hatchings can be generated by texture mapping. Such techniques are qualified for polygonal scenes. For other object kinds a special treatment is necessary, especially for free form surfaces, where a self occlusion without occluding edges is possible.
In case there are many surfaces with common borders present, as can arise from triangulating complex objects, not all border information should be used. Then for each edge has to be examined whether it is part of a border. This could be done by investigating the material properties for neighbouring objects. Another possibility is to introduce special object kinds for subdivided free form surfaces, a method that increases modeling and implementation efforts. The projection of hatching lines especially affords the calculation of curves in closed formulas.
A system that handles this kind of difficulties is proposed by Dooley and Cohen[7]. Objects in the scene are attached to a set of semantic attributes (importance, line style) that are interactively determined. The rendering algorithm works with illustration rules that are applied to the projected lines according to their attributes.
In what follows an image centered technique shall be investigated for its suitability to generate copper plates. Similar considerations to ameliorate presentation techniques for three dimensional scenes are presented by Saito and Takahashi[8], where an interim representation, the so called G-Buffer is used for storing a pixel image that contains additional scene information. Afterwards this representation is transformed into a black and white representation by appropriate operators.
 is the normalized
length from the start point to the intersection point. The geometric data,
the material description parameters and the illumination model determine
the resulting colour values (i.e. RGB) for the ray. For copper plates this
basic algorithm has to be modified, introducing new parameters into the
illumination formula. The geometrical values at the intersection point
are the basis for determining the lines for edges and hatchings of a copper
plate.
is the normalized
length from the start point to the intersection point. The geometric data,
the material description parameters and the illumination model determine
the resulting colour values (i.e. RGB) for the ray. For copper plates this
basic algorithm has to be modified, introducing new parameters into the
illumination formula. The geometrical values at the intersection point
are the basis for determining the lines for edges and hatchings of a copper
plate.
For each ray query the rendering process can be divided into the following phases:
 value in what follows. For each pixel
value in what follows. For each pixel  is calculated, stored in a pixel file, and later discretized to black and
white values with a simple threshold operator in the post processing step.
is calculated, stored in a pixel file, and later discretized to black and
white values with a simple threshold operator in the post processing step.
A first possibility is to calculate a value
if an intersection has taken place, where a0 is a newly introduced parameter in the material description class for the object that was hit. When the resulting pixel image is treated with a threshold operator the result is a interference pattern with a circular structure, caused by some properties of central projection. This method offers only few variation possibilities, as the direction of the hatchings cannot be changed.
The following suggestion comes close to the conventional texture techniques. The object that was hit by the query ray is geometrically overlayed with parallel, plane laminae (Figure 1). The laminae consist of shares of parallel and equidistant planes in 3D space. As an extension also other lamina objects are possible, e.g. sphere shells stacked into each other or whatever spatial texture.
Figure 1: Hatchings with the ray tracing method
Let t = <tx,ty, tz> the intersection
point of the query ray with an object: t = p +  · r. The lamina share i is described by the plane coefficients
ei,1,ei,2,ei,3,ei,4
of the first lamina and the distance parameter ai of
the parallelly placed laminae. Then the normalized distance bi
is given by:
· r. The lamina share i is described by the plane coefficients
ei,1,ei,2,ei,3,ei,4
of the first lamina and the distance parameter ai of
the parallelly placed laminae. Then the normalized distance bi
is given by:
fi := ei,1·tx + ei,2·ty + ei,3·tz + ei,4
bi is put out as pixel value and treated with a threshold operator in the postprocessing phase. A structure of parallel lines will then be seen on the object's surface.
Several hatches can be combined by summing up the values bi multiplied by the weight factor ci (a parameter in the material class). The hatches are first calculated separately and then later combined. Chosing negative factors ci (desirable) nullifications can be reached. Summing up two hatches will result in a typical triangle pattern after applying the threshold operator on the pixel image.
Overlay of two hatches without producing the triangle pattern is reached by applying the following operator:
In copper plates fluctuations of image values depending on the pixel value in the corresponding RGB image are expressed by different thickness of lines. To reach this we add a weighted amount of the RGB colour value. We introduce the parameters hf and hb to the material description class for scaling the brightness values. Be h the value of a weighted sum of the RGB value, then we add the term (h-hb) · hf to manipulate the thickness.
Be bi and ci weight factors that
are newly introduced parameters in the illumination formula. Then we get
the following formula for  using the parameter r from Equation 2
and bi from Equation 3:
using the parameter r from Equation 2
and bi from Equation 3:
Edges are sudden changes in the image domain, that are difficult to determine with an image centered method. Often neighbouring pixel values are combined with an edge detection operator in image domain. The resulting image depends on the illumination formula and the illumination situation. Alternatively changes of the material description class or of the object id in neighbouring pixels can be marked. For drawing shadows the number of visible light sources can be given out.
By using the  value
in an edge detection operator sudden depth changes are detected. But it
is undesirable that also objects with a normal vector nearly perpendicular
to the query rays are marked. Common edges of neighbouring polygons (e.g.
polyhedra) cannot be detected with this method.
value
in an edge detection operator sudden depth changes are detected. But it
is undesirable that also objects with a normal vector nearly perpendicular
to the query rays are marked. Common edges of neighbouring polygons (e.g.
polyhedra) cannot be detected with this method.
As the  value only varies
in a small range, and the query ray is relatively long, the control input
for the algorithm must contain a range for scaling the
value only varies
in a small range, and the query ray is relatively long, the control input
for the algorithm must contain a range for scaling the 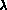 value. An automatic determination is not possible, as there is no global
reference in the scene.
value. An automatic determination is not possible, as there is no global
reference in the scene.
Sudden changes of the value 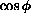 ,
i.e. the angle between query ray and normal vector, are marked. Actually,
it is better to use the value
,
i.e. the angle between query ray and normal vector, are marked. Actually,
it is better to use the value 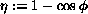 instead, to avoid the use of negative factors in second order rays. This
method can detect edges of neighbouring polygons and strongly curved objects,
but no sudden changes in depth. Disadvantages are given by the non linearity
of this value. This operator is blind with respect to direction. Therefore
in some situations edges cannot be detected. To avoid this, the normal
vector can be put out in three separate channels.
instead, to avoid the use of negative factors in second order rays. This
method can detect edges of neighbouring polygons and strongly curved objects,
but no sudden changes in depth. Disadvantages are given by the non linearity
of this value. This operator is blind with respect to direction. Therefore
in some situations edges cannot be detected. To avoid this, the normal
vector can be put out in three separate channels.
Pixels can also be marked when the distance of the intersection point to the object border is smaller than a given threshold. This works only when polygonal scenes are used, but not on objects with curvatures or on combined objects. This method does not need information on neighbouring pixels. Near the edges the minimum of the distance values has to be chosen; but this makes only sense for convex polygons.
To get a satisfactory result several of the proposed types of information
have to be merged. Actually, one can get good results when combining the
edge-detected 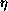 and
and 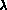 .
.
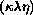 were treated similar to the RGB values, i.e. they were scaled by a factor
and then added. This holds for
were treated similar to the RGB values, i.e. they were scaled by a factor
and then added. This holds for 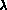 and
and 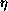 . For
. For  similar to the overlay of laminae bothering triangle pattern appear. To
avoid this we use the
similar to the overlay of laminae bothering triangle pattern appear. To
avoid this we use the  operator
from Equation 4.
operator
from Equation 4.
Be 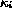 the value for the
current ray generation according to Equation 5,
the value for the
current ray generation according to Equation 5,  the value for the jth ray (reflection, refraction, xray) in
generation i, and accordingly ci,j and di,j
factors from the material description class. Then
the value for the jth ray (reflection, refraction, xray) in
generation i, and accordingly ci,j and di,j
factors from the material description class. Then 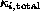 calculates from
calculates from
Thus hatchings and border lines can be exposed on mirror surfaces and
through glass objects. For modeling with second order rays we propose some
design rules. The object that is the mirror should have no hatches or only
hatches with a wide distance, so as not to interfere with the finer grain
hatches of the objects in the mirror. When chosing scaling factors ci,j,
di,j less than 1.0 for the  value, the hatchings in the mirror will appear thinner than usual (thicker
when using factors greater than 1.0). For the
value, the hatchings in the mirror will appear thinner than usual (thicker
when using factors greater than 1.0). For the 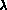 and
and 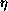 values one should be
aware that the value can reach the maximal value. The
values one should be
aware that the value can reach the maximal value. The 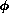 value would be critical in this case as it is 1.0 for planes perpendicular
to the query ray. Therefore we use
value would be critical in this case as it is 1.0 for planes perpendicular
to the query ray. Therefore we use 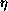 instead to avoid negative scale factors.
instead to avoid negative scale factors.
For readers unfamiliar with image processing algorithms we will refer to introducing textbooks on the subject[5]. Mainly a threshold operator, and convolution algorithms with different stencils will be used, e.g an approximation of the Gauß-Laplacian and the Kirsch-Compass operator.
Especially when using low resolutions and fine grain hatches there is a danger of interference patterns and alias problems. The characteristics of the images will be different when printed on different output media: while these images resemble copper plates on laser printers they look like woodcuts on pin printers.
As conventional copper plates have no grey values a black and white
representation can be convenient, if the resolution ist high enough. At
low resolution severe aliasing problems occur, especially with hatches.
If all channels are anti-aliased (especially  )
then the postprecessing can be adapted to deliver grey values, using a
threshold for each grey value.
)
then the postprecessing can be adapted to deliver grey values, using a
threshold for each grey value.
To investigate the aliasing problems a series of original copper plates werde scanned in at various resolutions. Using high resolution all lines were reproduced, while the low resolution images had more the look of an ordinary grey scale image, and the characteristic copper plate hatches disappeared. So the hatches information is very sensitive with respect to the alias effect.
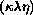 values in the range 0..255.
values in the range 0..255.
In the current implementation the formula 5 is fully implemented with the restriction that three lamina shares can be specified. The syntax of the new parameters in the VERA input language is given in Appendix A.
The calculation of the final result is done in a separate image processing program, in order not to change the structure of the ray tracer too much. Threshold and edge detection operators are used channelwise. The resulting bitmaps are merged bitwise by an or-Operator.
Figure 2: A sphere with different hatchings and as (dithered) raster image
To illustrate the potential of the new technique a sphere is treated with different hatches in Figure 2. The sphere is illuminated from the upper right side. A glossy spot can be seen in the reproduction of the RGB pixel image. Upper: hatching without (1a) and with brightness modulation (1b), two hatchings added without (2a) and with brightness modulation (2b). The characteristic triangle pattern can be seen. Lower: two hatchings overlayed without (3a) and with brightness modulation (3b). Using a negative weight factor for the second hatching, inverse lines and special patterns can be produced (4).
Note: The original images of the article are not presented here. We show some other images instead, that are more propriate for a Web-document. Until these are prepared, we refer to a document on nonrealistic rendering.
The copper plate method has been adapted for making icons. Caused by the low resolution of the icons there is a danger for interferences between the hatchings and the image raster, and there is nearly no possibility for anti rastering methods in this case. The designer should be aware of this while modeling.
Note: The illustration images are currently under preparation
The next step could be to research how to use this technique for computer animations. This is also interesting in connection with interaction techniques, where short animation sequences can be shown in icons. Especially the problems occurring due to motion blur and interferences should be inquired. It could also be interesting to use this technique in visualization technique.